Alegeri parlamentare

Putere de vot în Parlamentul României după alegerile din 2012
 

CIPRIAN NIŢU
[West University of Timișoara]

Abstract:
This article aims to investigate the voting power of political groups in Romanian Parliament after elections held in December 2012. Using some classical indeces of voting power such as Shapley-Shubik, Banzhaf and Coleman indices, the paper leads to the conclusion that the relative power of political groups within Parliament significantly varies from voting weights that these groups have as a result of the election outcome.

Keywords: Romanian Parliament; political groups; voting power; power indices; voting weights

Analiza puterii de vot în Parlamentul României. Indici ai puterii de vot

Cercetarea de faţă îşi propune să analizeze puterea de vot a grupurilor politice din Parlamentul României generate în urma alegerilor din decembrie 2012. Analiza utilizează câţiva indici (clasici) care măsoară puterea de vot a membrilor unui organism decizional. Aceşti indici au fost propuşi în literatura de specialitate pentru a măsura puterea de vot a jucătorilor care deţin ponderi diferite ale voturilor în cadrul unor astfel de organisme decizionale. De multe ori,  atât la nivelul nespecialiştilor, cât şi la nivelul specialiştilor în ştiinţele politice, puterea de vot a unui astfel de jucător este echivalată cu ponderea voturilor pe care le deţine acesta în cadrul mecanismului decizional. Ori, indicii puterii de vot (care pleacă întotdeauna de la o modalitate particulară de conceptualizare a puterii) sugerează că influenţa (puterea) unui actor ce deţine o anumită pondere a voturilor în cadrul procesului decizional, poate fi mai mare sau mai mică decât respectiva pondere. Aşa cum constată D. Leech,

„puterea de facto a unui membru depinde nu doar de numărul voturilor pe care le are acesta, ci şi de configuraţia completă a voturilor alocate tuturor membrilor organismului respectiv. Pentru a măsura puterea este necesară calcularea unui indice de putere care ia în considerare toate aceste voturi. Un indice de putere măsoară influenţa relativă a fiecărui membru asupra procesului de luare a deciziilor, în sensul abilităţii sale de a-şi folosi votul astfel încât să transforme o coaliţie a altor membrii din una care nu satisface criteriul majorităţii într-una care satisface acest criteriu, şi care devine astfel câştigătoare. Numărul cazurilor în care un membru poate face acest lucru este exprimat ca proporţie a cazurilor în care poate apărea o astfel de coaliţie câştigătoare. [Ca expresie de tip probabilist], un indice de putere măsoară puterea unui jucător în sens a priori [şi] nu poate fi folosit pentru a prezice anumite rezultate particulare, dar poate fi folosit pentru a înţelege şi propune diverse mecanisme decizionale în termenii puterii relative a membrilor.]”¹

Pentru a calcula puterea (influenţa) grupurilor parlamentare din Parlamentul României rezultate în urma alegerilor parlamentare de la finele anului 2012, am plecat de la câteva presupuneri care creează o situaţie ideală de vot. Am presupus astfel că prezenţa la vot este de 100%, că parlamentarii votează solidar cu grupul parlamentar din care fac parte şi că nu există coaliţii ideologice sau electorale între grupurile parlamentare. Această simplificare (idealizare) a situaţiei permite analiza puterii de vot a grupurilor parlamentare ca actori individuali şi, mai mult, poate fi privită ca o expresie a voinţei populare care a înzestrat partidele cu o putere relativă în cadrul legislativului.

Alegerile parlamentare din 2012 au generat următoarea structură a grupurilor celor două camere ale Parlamentului României. Din totalul de 412 locuri în Camera Deputaţilor PSD a obţinut 160 locuri (38,83%), PNL 101 locuri (24,51%), PDL 55 locuri (13,35%), PP-DD 45 locuri (10,92%), UDMR 18 locuri (4,37%), minorităţile 18 locuri (4,37%), PC 15 locuri (3,64%). Din totalul de 175 de locuri în Senat PSD a obţinut 64 locuri (36,57%), PNL 50 locuri (28,57%), PDL 24 locuri (13,71%), PP-DD 21 locuri (12%), UDMR 9 locuri (5,14%), PC 15 locuri (3,64%)².

Atunci când încercăm să aflăm care este puterea relativă de vot în Parlament, pe lângă numărul grupurilor şi ponderea voturilor lor, e important să luăm în considerare şi procedurile de vot care impun cote diferite ale votului pentru adoptarea unei decizii şi, astfel, modifică puterea relativă a actorilor. Conform regulamentelor de organizare şi funcţionare ale celor două Camere ale Parlamentului României, în condiţiile existenţei cvorumului legal, un proiect de lege sau propunere legislativă se adoptă conform următoarei proceduri: dacă propunerea legislativă în cauză se referă la un proiect de modificare a Constituţiei, atunci aceasta este adoptată cu o majoritate de cel puţin 2/3 din numărul membrilor fiecărei Camere; dacă propunerea legislativă se referă la o lege organică, aceasta este adoptată cu votul majorităţii absolute a membrilor fiecărei camere; dacă propunerea legislativă vizează o lege ordinară, aceasta este adoptată cu votul majorităţii simple a membrilor fiecărei Camere³. Întrucât, aşa cum am menţionat mai sus, ne intereasă o situaţie ideală de vot, cazurile de boicot sau lipsă a cvorumului nu fac obiectul analizei de faţă. De asemenea, deoarece presupunem prezenţa completă la votul plenului, diferenţa între majoritatea simplă şi cea absolută devine irelevantă. Ce ne interesează însă în continuare este diferenţa între deciziile care presupun majoritatea de cel puţin 2/3 şi 1/2 din numărul voturilor din cele două Camere.

Lucrarea va discuta în continuare indicii puterii de vot care stau la baza analizei (aceştia fiind Shapley-Shubik, Banzhaf şi Coleman), urmând ca apoi, pe baza calculului acestor indici pentru fiecare grup parlamentar, să fie evidenţiate unele aspecte privitoare la de puterea de vot a grupurilor din Camera Deputaţilor şi Senatului României.

Indicele Shapley-Shubik

Indicele Shapley-Shubik⁴ are la bază două concepte importante: cel de „coaliţii secvenţiale” care se pot forma între membrii unui organism decizional şi cel de „jucător-pivot” (pivotal player). În cazul coaliţiilor secvenţiale, spre deosebire de coaliţiile non-secvenţiale cum vom vedea mai jos, se iau în calcul toţi jucătorii precum şi ordinea în care actorii intră într-o astfel de coaliţie. Dacă notăm jucătorii (grupurile parlamentare în cazul nostru) cu G, <G1, G2, G3> şi <G3, G1, G2> se referă la două coaliţii secvenţiale diferite în cazul unui sistem cu 3 jucători. În acest caz <G1, G2>, de exemplu, nu reprezintă o coaliţie secvenţială. Pentru un joc cu minim 3 jucători (indicele Shapley-Shubik nu se aplică la un joc cu 1 sau 2 jucători) avem 6 coaliţii secvenţiale exprimate prin factorialul numărului 3 (3!). Factorialul unui număr întreg n este notat cu n! şi este egal cu produsul numerelor întregi mai mici sau egale cu n

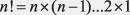
sau

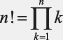
Jucătorul „pivot” în cazul coaliţiilor secvenţiale este acel jucător unic care, prin votul său în sprijinul coaliţiei în momentul intrării, transformă respectiva coaliţie dintr-una pierzătoare într-una câştigătoare⁵. Indicele Shapley-Shubik măsoară puterea unui jucător luând în considerare cazurile în care acesta apare ca jucător pivot (raportat la numărul coaliţiilor secvenţiale).

Pentru a calcula indicele de putere al jucătorului p trebuie făcuţi următorii paşi: 1) se face lista tuturor coaliţiilor secvenţiale ce conţin toţi cei n jucători (există n! coaliţii); 2) pentru fiecare coaliţie secvenţială se determină jucătorul pivot; 3) se numără de câte ori p este jucător pivot, iar acest număr se notează cu 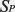; 4) se calculează raportul , care reprezintă indicele Shapley-Shubik (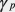) pentru jucătorul p.

Pentru exemplificare să presupunem sistemul format din 3 jucători [10: 3, 5, 9], unde cota q (numărul voturilor necesare pentru a forma o majoritate) este 10, iar ponderea voturilor celor trei jucători G1, G2, G3 este 3, 5, respectiv 9. În acest caz avem şase coaliţii secvenţiale posibile în cadrul cărora jucătorul G3 apare de patru ori ca jucător-pivot, în timp ce jucătorii G1 şi G2 apar o singură dată ca jucători-pivot. Astfel indicele de putere pentru G1 şi G2 este de 1/6 (adică 0,16666), iar pentru G3 este de 4/6 (adică 0,66666). 

Formula indicelui Shapley-Shubik poate fi definită în felul următor⁶:

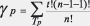
unde p = 1, ... , n; operatorul Σ se referă la suma cazurilor în care jucătorul p are rol de jucător-pivot (Tp), T fiind o submulţime a lui N (mulţimea tuturor jucătorilor); t este numărul membrilor lui Tp, iar n este numărul membrilor lui N. Formula indicelui Shapley-Shubik exprimă probabilitatea ca jucătorul p să deţină statutul de jucător-pivot în cadrul coaliţiilor formate în mod aleator şi reprezintă astfel un indicator al puterii sale de a schimba prin vot sensul unei decizii particulare. Trebuie precizat faptul că indicele de putere se calculează pentru fiecare jucător în parte, iar suma indicilor de putere a tuturor jucătorilor trebuie să fie 1. Cota şi ponderile sunt numere întregi (fapt pentru care în calculul de mai jos al valorilor indicelui corespunzător grupurilor politice din Parlamentul României, ponderile grupurilor parlamentare vor fi rotunjite fără zecimale).

Indicele Banzhaf

Distribuţia puterii calculată cu ajutorul indicelui Banzhaf⁷ poate fi diferită de cea calculată cu ajutorul indicelui Shapley-Shubik deoarece el conceptualizează diferit puterea sau influenţa unui actor.  Ca şi indicele Shapley-Shubik , indicele Banzhaf exprimă probabilitatea ca votul unui jucător să modifice rezultatul în cadrul unor sisteme electorale sau de luare a deciziilor în care voturile actorilor nu au ponderi egale. Spre deosebire de primul însă, indicele Banzhaf ia în considerare toate coaliţii non-secvenţiale posibile, indiferent de mărime. Pentru Banzhaf {G1, G2, G3} şi {G3, G2, G1} este una şi aceeaşi coaliţie, spre deosebire de Shapley-Shubik unde ele reprezintă coaliţii diferite. De asemenea, Banzahaf foloseşte noţiunea de „jucător-cheie” (critical player), nu pe cea de „jucător-pivot”, acesta fiind acel jucător care poate determina prin votul său eşecul unei măsuri.

Pentru a calcula puterea de vot a unui actor cu ajutorul indicelui Banzhaf trebuie identificate toate coaliţiile câştigătoare din cadrul coaliţiilor posibile formate din minim 2 jucători (înţelese ca şi combinaţii de n jucători luaţi câte k în care ordinea jucătorilor nu este importantă) şi identificat numărul votanţilor-cheie. Dacă luăm ca exemplu următorul sistem simplu cu patru jucători [6: 4, 3, 2, 1], unde cota q (numărul voturilor necesare pentru a lua o decizie) este 6, iar ponderea voturilor celor patru jucători G1, G2, G3, G4 este 4, 3, 2, respectiv 1, numărul coaliţiilor posibile este 11 şi se calculează cu ajutorul formulei

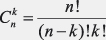
unde n este numărul jucătorilor, iar k = 2, 3, 4. Din aceste combinaţii (coaliţii) posibile şapte sunt câştigătoare, iar numărul votanţilor cheie este 0, 1, 2 sau 3, în funcţie de combinaţie. Coaliţiile câştigătoare în acest exemplu sunt următoarele (jucătorii-cheie fiind cei subliniaţi): {G1, G2, G3},{G1, G2, G4},{G1, G3, G4},{G2, G3, G4},{G1, G2},{G1, G3},{G1, G2, G3, G4}. După cum se poate observa din acest exemplu, indicele Banzhaf interpretează altfel decât indicele Shapley-Shubik cazurile în care un jucător poate să influenţeze rezultatul votului, astfel că probabilitate ca un jucător să transforme o coaliţie formată în mod aleator dintr-una câştigătoare într-una pierzătoare este calculată conform formulei (Banzhaf absolut)

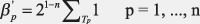
sau formulei (Banzhaf normalizat)

unde probabilitatea unui subset al lui N, (Tp) este acum 21-n şi nu t!(n-t-1)! ca în cazul indicelui Shapley-Shubik⁸.

Indicii Coleman

James Coleman critică viziunea cu privire la putere exprimată prin intermediul indexului Shapley-Shubik şi, în general, prin teoria jocului⁹, dar prezintă o afinitate mai mare cu indicele Banzhaf (unii autori preferă chiar să se refere la indicele Banzhaf-Coleman)¹⁰. Coleman optează pentru o concepţie cu privire la putere ca „acţiune” şi nu ca „împărţire a prăzii”. Astfel Coleman renunţă la condiţia specifică teoriei jocului ca suma indicilor de putere a membrilor să fie o constantă (1). Altfel spus, Coleman concepe puterea în termeni absoluţi, nu relativi. Coleman mută accentul de la puterea membrilor în relaţiile dintre ei, la relaţia existentă între puterea membrilor şi cea a organizaţiei în interiorul căreia aceştia acţionează. El introduce trei concepte: puterea de vot a organizaţiei, puterea „negativă” a unui membru de a împiedica o acţiune şi puterea „pozitivă” a unui membru de a iniţia o acţiune¹¹.

Să presupunem că avem o colectivitate formată din n membri, N = {1, 2, …, n}. În cazul oricărei decizii adoptate vor exista s membri care votează „pentru” şi n membri care votează „împotrivă”. Membrii care votează „pentru” formează submulţimea S a acestei colectivităţi, S⊆N, numărul acestora fiind exprimat prin w(S), iar numărul celor care votează „împotrivă” prin w(N/S). Decizia este luată dacă w(S)= q. Dacă notăm cu ω submulţimea rezultatelor care conduc la acţiune (adoptarea deciziei), un membru p poate schimba rezultatul votului dacă există o submulţimeS astfel încât q −wp= w(S) < q. Numărul subseturilor în cazul cărora p poate schimba rezultatul votului este notat cu ηp.

Puterea organizaţiei de a acţiona (A) este numărul relativ al rezultatelor care conduc la acţiune: A = ω/2n. Din 2n rezultate posibile în ω cazuri votul majoritar conduce la acţiune. Notaţia A reprezintă probabilitate apariţiei unui astfel de vot câştigător. În cazul luării deciziilor prin unanimitate (altfel spus când toţi membrii trebuie să voteze „pentru” ca decizia să fie adoptată) ω = 1 şi A =2-n. Când n este mare puterea de acţiune a  organizaţiei este foarte mică. În cazul luării deciziilor prin regula majorităţii simple unde q = w(N)/2, puterea organizaţiei de a acţiona este maximă (A =1/2), jumătate din rezultatele voturilor conducând la acţiune, ω = 2n-1.

Puterea unui membru de a preveni acţiunea (Pp) se referă la capacitatea unui membru p de a împiedica luarea deciziei prin votarea împotriva unui grup care devine astfel din unul câştigător unul pierzător:    

Pp=ηp/ω

unde p = 1, ..., n; ω este numărul submulţimilor câştigătoare; iar ηp este numărul cazurilor în care p transformă o submulţime câştigătoare într-una pierzătoare.

Puterea unui membru de a iniţia acţiunea (Ip) reprezintă capacitatea unui membru p de a contribui la luarea deciziei prin votarea alături de un grup care devine astfel din unul pierzător unul câştigător.

UIp= ηp/(2n-ω)

unde p = 1, ..., n; 2n-ω reprezintă numărul submulţimilor pierzătoare; iar ηp este numărul cazurilor în care p transformă o submulţime pierzătoare într-una câştigătoare.

Observăm din această descriere a tipurilor de putere la Coleman că un jucător care are puterea totală (Pp=1)de a împiedica o decizie, ponderea voturilor sale fiind mai mare decât majoritatea necesară (q), nu are în mod necesar o putere similară de a iniţia o acţiune. Ideea călăuzitoare în propunerea acestor indici de către Coleman este că, indiferent de procedura de vot, indiferent de modul în care este definită majoritatea necesară pentru adoptarea unei decizii (cota, q), fie ea majoritate simplă sau calificată, nu va exista doar un grup câştigător al votului, în timp ce restul membrilor formează un grup pierzător. Definind puterea în termeni absoluţi, Coleman consideră că fiecare actor are partea sa de influenţă, mai mare sau mai mică. Acest lucru ne ajută, consideră D. Leech, 

„să înţelegem de ce există multe organisme decizionale sau situaţii care angajează o colectivitate în direcţia acţiunii în condiţiile în care cota este mai mică decât jumătate din ponderea totală a voturilor, sau faptul că există atât reguli de vot simetrice (majoritate simplă), cât şi reguli de vot asimetrice (supermajoritate, vot majoritar calificat, sau proceduri care necesită mai puţin de jumătate din numărul voturilor)”¹².

Puterea de vot a grupurilor din Camera Deputaţilor şi Senat

Calculul valorii indicilor de putere (Shapley-Shubik, Banzhaf şi Coleman) pentru Camera Deputaţilor şi Senat este redat în tabelele de mai jos. Indicii au fost calculaţi atât pentru situaţia în care luarea deciziei necesită cel puţin 1/2 din totalul voturilor cât şi pentru situaţia în care decizia necesită cel puţin 2/3 din totalul voturilor.

Concluzii

Observăm din valorile indicilor că ipoteza iniţială, conform căreia puterea (influenţa) grupurilor nu este egală cu ponderea voturilor pe care o deţine diferitele partide politice, este confirmată. Observăm, de exemplu, că probabilitatea ca grupul parlamentar al PSD să transforme o presupusă coaliţie pierzătoare într-una câştigătoare este mai mare decât ponderea voturilor pe care o are acest partid, atât la Camera Deputaţilor, cât şi în Senat, indiferent de cota (q) necesară pentru adoptarea unei legi. Această probabilitate este mai apropiată de valoarea ponderei voturilor în Senat, în cazul deciziilor care necesită o majoritate „simplă” a voturilor (1/2). Surprinzător este faptul că puterea PNL în Camera Deputaţilor de a transforma o potenţială coaliţie pierzătoare într-una câştigătoare este egală cu cea a PDL, chiar dacă ponderea voturilor este aproape dublă, în cazul proiectelor de lege ce necesită adoptarea lor cu cel puţin 1/2 din totalul voturilor. Raportat la numărul voturilor, PDL are o putere mai mare decât PNL de a transforma o coaliţie pierzătoare într-una câştigătoare atunci când cota necesară este 1/2. Raportul dintre PNL şi PDL în ceea ce priveşte puterea de vot se echilibrează atunci când cota este 2/3. Observăm de asemenea că indicele Shapley-Shubik este acelaşi pentru PDL şi PP-DD atunci când cota este de 2/3, chiar dacă ponderea voturilor lor este diferită (13, respectiv 11%). Se poate observa şi faptul că partidele mici au o influenţă mai mică în formarea coaliţiilor câştigătoare decât simpla pondere a voturilor (cu excepţia PC la Senat când cota este de 1/2).

În ceea ce priveşte puterea grupurilor de a transforma o potenţială coaliţie câştigătoare într-una pierzătoare, observăm că aceasta înregistrează o creştere pentru grupurile mici, în timp ce PSD, partidul cel mai mare, înregistrează o valoare a indicelui Banzhaf pentru cota de 1/2 apropiată de cea a indicelui Shapley-Shubik, însă înregistrează o scădere semnificativă de aproximativ 10% pentru o cotă de 2/3, atât la Camera Deputaţilor, cât şi la Senat. Situaţia pentru PNL şi PDL se repetă, în mare, în jurul aceloraşi valori. La fel şi în cazul PDL şi PP-DD (atunci când cota este de 2/3, cele două partide au o putere egală în ceea ce priveşte împiedicarea formării unei coaliţii câştigătoare).  

În ceea ce priveşte indicii Coleman, puterea jucătorilor de a împiedica o acţiune este substanţial mai mare pentru jucătorii mari. PSD de exemplu are un indice de 0,75 la Camera Deputaţilor şi 0,64 la Senat (când cota este 1/2) şi 1 atât la Camera Deputaţilor, cât şi la Senat  când cota este de 2/3. Puterea PSD de iniţiere a unei acţiuni scade însă dramatic atunci când cota este de 2/3, revenind foarte aproape de ponderea voturilor pe care PSD o deţine în cele două camere. Interesant din nou, PNL şi PDL au la Camera Deputaţilor o putere egală de prevenire şi iniţiere a unei acţiuni, atunci când cota este 1/2. La Senat raportul dintre cele două rămâne echilibrat atât în ceea ce priveşte împiedicarea, cât şi iniţierea unei acţiuni, atâta timp cât cota este 1/2. Raportul este însă în favoarea PNL atunci când cota este de 2/3, fie că e vorba despre împiedicarea unei acţiuni, fie că este vorba despre iniţierea unei acţiuni. Partidele mai mici au o putere mai mare de împiedicare a unei acţiuni (mai mare atunci când cota este 2/3) şi de iniţiere (când cota este 1/2) la Senat, însă au o putere mult mai mică de a iniţia o acţiune (atunci când cota este 2/3) la Camera Deputaţilor.

Bibliografie
BANZHAF, John F., „Weighted voting doesn’t work: A mathematical analysis,” Rutgers Law Review 19, 2 (1965): 317-343.
COLEMAN, James S., „Control of Collectivities and the power of a collectivity to act”, în Bernhardt Lieberman (coordonator), Social Choice (New York: Gordon and Breach, 1971), 269-300.
LEECH, Dennis, „An Empirical Comparison of the Performance of Classical Power Indices,” Political Studies 50,1 (2002): 1-22.
LEECH, Dennis, „The use of Coleman’s power indices to inform the choice of voting rule with reference to the IMF governing body and the EU Council of Ministers” (research paper, 2002: 11-2),  http://www2.lse.ac.uk/CPNSS/projects/VPP/VPPpdf/vpppublications/vpp02_07.pdf, accesat 15.02.2013.
SHAPLEY, Lloyd S., SHUBIK, Martin, „A method for evaluating the distribution of power in a committee system,” American Political Science Review 48 (1954): 787-792.
*** „Structura Parlamentului României”, http://www.cdep.ro/pls/parlam/structura.gp?leg=2012, accesat 06.02.2013.
***„Organizarea şi funcţionarea celor două Camere ale Parlamentului României”, http://www.cdep.ro/pls/dic/site.page?den=introcd1-i, accesat 06.02.2013.

NOTE

CIPRIAN NIŢU – asistent universitar la facultatea de Ştiinţe Politice, Filosofie şi Ştiinţe ale Comunicării a Universităţii de Vest din Timişoara. Este doctorand al Facultăţii de Ştiinţe Politice a Universităţii din Bucureşti. Din 2009 este editor al revistei Political Studies Forum, revistă ce apare sub egida departamentului de Știinţe Politice din cadrul Facultății de Ştiinţe Politice, Filosofie şi Ştiinţe ale Comunicării a Universitatea de Vest din Timișoara.

 sus